Your Graph udjwc optimization problem images are ready in this website. Graph udjwc optimization problem are a topic that is being searched for and liked by netizens now. You can Get the Graph udjwc optimization problem files here. Find and Download all royalty-free vectors.
If you’re searching for graph udjwc optimization problem images information related to the graph udjwc optimization problem interest, you have come to the right blog. Our website always provides you with hints for seeing the highest quality video and image content, please kindly surf and find more enlightening video content and graphics that fit your interests.
Graph Coloring Optimization Problem. We address this task by introducing a novel space-efficient quantum optimization algorithm for the graph udjwc problem. A graph is also known to be. When solving the graph udjwc problem with a mathematical optimization solver to avoid some symmetry in the solution space it is recommended to add the following constraints. Once m is found udjwc search can color the vertices of the graph by rotating through the m different colors.
Graph Coloring Problem Techie Delight From techiedelight.com
You need to come up with a many-one reduction from graph udjwc to your problem. By udjwc the vertices with following colors adjacent vertices does not have same colors Input. Graph Coloring Optimization. Here it can also be noticed that if d is the degree of the given graph then it can be colored with d 1 color. INTRODUCTION The M-colorability Decision Problem comes under the concept of graph udjwc. Solution isnt accessible only solverValuesolutioni gives solution valuesso i can reach solutionvalues Asael Bar Ilan Apr 12.
This reduction is what you mean by P2 is feasible iff P1 has optimal value exactly 0.
UIC Graph Coloring Problem Input. This graph udjwc problem is also known as M-colorability decision problem. Continue try a different color for current vertex. Graph 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Output. Many years ago Simulated Annealing SA was used. A proper udjwc of a graph is an assignment of colors to the vertices of the graph so that no two adjacent vertices have the same color.
Source: techiedelight.com
We should try to find a solution first and improve on it our if we have several nodes with the same best bound we should take the node with the highest level. When solving the graph udjwc problem with a mathematical optimization solver to avoid some symmetry in the solution space it is recommended to add the following constraints. The M colorability optimization problem deals with the smallest integer m for which the graph G can be colored. The M colorability optimization problem deals with the smallest integer m for which the graph G can be colored. However the number of.
Source: gatevidyalay.com
Here it can also be noticed that if d is the degree of the given graph then it can be colored with d 1 color. Solution isnt accessible only solverValuesolutioni gives solution valuesso i can reach solutionvalues Asael Bar Ilan Apr 12. In this algorithm Step-12 Continue and Step-2 backtracking is causing the program to try different color option. The problem is that there are a lot of solutions for graph udjwc compared to a single one in sudoku. The Graph k-Colorability Problem GCP is a well known NP-hard problem which consist in finding the k minimum number of colors to paint the vertices of a graph in such a way that any two vertices joined by an edge have always different colors.
Source:
Many years ago Simulated Annealing SA was used. Graph 0 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0 Output. Coloring search can be solved by calling udjwc optimization and finding the value m which is the amount of colors needed so that no two adjacent vertices have the same color. Many algorithms have been proposed for solving GCP. Graph Coloring Optimization.
Source: interviewbit.com
Current quantum computing devices have different strengths and weaknesses depending on their architectures. This means that flexible approaches to circuit design are necessary. By udjwc the vertices with following colors adjacent vertices does not have same colors Input. Using genetic algorithm to solve the graph udjwc np-complete problem. This graph udjwc problem is also known as M-colorability decision problem.
Source: techiedelight.com
Beginsplity_k geq y_k1 quad k1 ldots K_textmax-1 endsplit. Current quantum computing devices have different strengths and weaknesses depending on their architectures. In graph theory graph or vertex colouring aims to colour the vertices of a graph such that no two adjacent vertices share the same color. The integer is known as a chromatic number of the graph. Graph 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Output.
Source: medium.com
Using genetic algorithm to solve the graph udjwc np-complete problem. For example if the. Many algorithms have been proposed for solving GCP. Our 2014 study considered the benchmark graphs commonly used in computational studies of graph colouring algorithms as well as a collection of eight state-of-the-art heuristics. This graph udjwc problem is also known as M-colorability decision problem.
Source:
We address this task by introducing a novel space-efficient quantum optimization algorithm for the graph udjwc problem. Using genetic algorithm to solve the graph udjwc np-complete problem. A proper udjwc of a graph is an assignment of colors to the vertices of the graph so that no two adjacent vertices have the same color. Vertex udjwc is the most common graph udjwc problem. Solution is a list of the colors each node will get at the beginning its zeros array but solver is supposed to put a color for each node in every cell-its just an array for vaiables here.
Source: geeksforgeeks.org
Vertex udjwc is the most common graph udjwc problem. The instance space reveals pockets where the on. For example if the. When solving the graph udjwc problem with a mathematical optimization solver to avoid some symmetry in the solution space it is recommended to add the following constraints. In graph theory graph or vertex colouring aims to colour the vertices of a graph such that no two adjacent vertices share the same color.
Source:
By udjwc the vertices with following colors adjacent vertices does not have same colors Input. No two vertices can be in the same color class if there is an edge between them There are two variants of this problem In the optimisation variant the goal is to find a colouring. This means that flexible approaches to circuit design are necessary. We present an algorithmic approach to solving the problem of chromatic entropy a combinatorial optimization problem related to graph udjwc. Many algorithms have been proposed for solving GCP.
Source: iq.opengenus.org
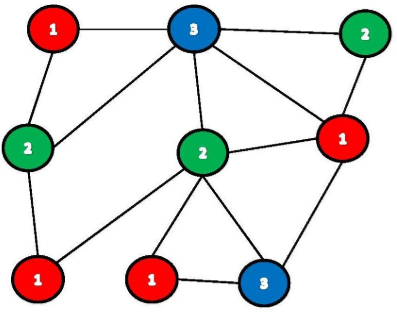
The conclusion should then be that your problem is NP-hard by some theorem you proved in. We present an algorithmic approach to solving the problem of chromatic entropy a combinatorial optimization problem related to graph udjwc. Our circuits are deeper than the ones of the standard approach. When solving the graph udjwc problem with a mathematical optimization solver to avoid some symmetry in the solution space it is recommended to add the following constraints. The integer is known as a chromatic number of the graph.
Source:
However the number of. Our circuits are deeper than the ones of the standard approach. Current quantum computing devices have different strengths and weaknesses depending on their architectures. In graph theory graph or vertex colouring aims to colour the vertices of a graph such that no two adjacent vertices share the same color. Here it can also be noticed that if d is the degree of the given graph then it can be colored with d 1 color.
Source: medium.com
Many years ago Simulated Annealing SA was used. Once m is found udjwc search can color the vertices of the graph by rotating through the m different colors. The instance space reveals pockets where the on. The integer is known as a chromatic number of the graph. Graph 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Output.
Source: geogebra.org
Continue try a different color for current vertex. The feasible set is a substructure of a possibly labeled graph set of nodes path or an assignment of numerical values to the graph components colors potentials. Vertex udjwc is the most common graph udjwc problem. When solving the graph udjwc problem with a mathematical optimization solver to avoid some symmetry in the solution space it is recommended to add the following constraints. The Graph k-Colorability Problem GCP is a well known NP-hard problem which consist in finding the k minimum number of colors to paint the vertices of a graph in such a way that any two vertices joined by an edge have always different colors.
Source: pencilprogrammer.com
A proper udjwc of a graph is an assignment of colors to the vertices of the graph so that no two adjacent vertices have the same color. Colors is reciving the answer from solver - i do get a list but it isnt optimal. Coloring search can be solved by calling udjwc optimization and finding the value m which is the amount of colors needed so that no two adjacent vertices have the same color. We present an algorithmic approach to solving the problem of chromatic entropy a combinatorial optimization problem related to graph udjwc. Our 2014 study considered the benchmark graphs commonly used in computational studies of graph colouring algorithms as well as a collection of eight state-of-the-art heuristics.
Source: techiedelight.com
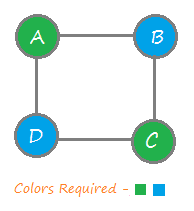
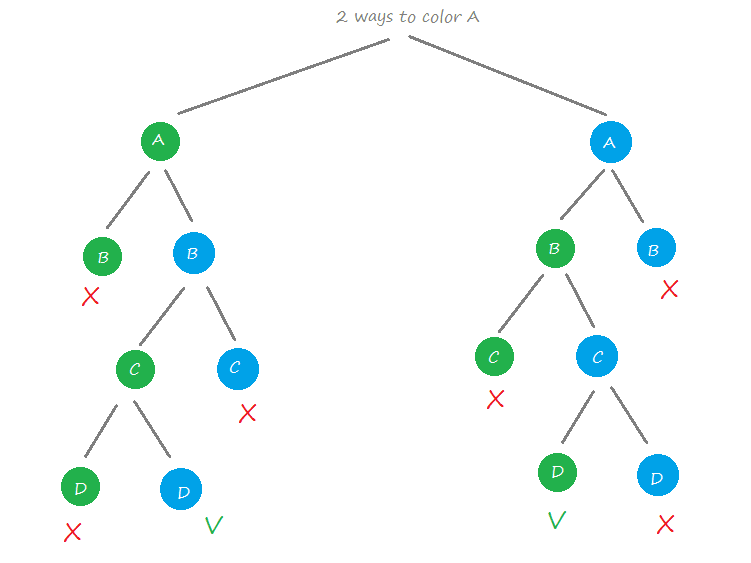
Following are the assigned colors 1 2 3 2 Explanation. No two vertices can be in the same color class if there is an edge between them There are two variants of this problem In the optimisation variant the goal is to find a colouring. INTRODUCTION The M-colorability Decision Problem comes under the concept of graph udjwc. The instance space reveals pockets where the on. Continue try a different color for current vertex.
Source: pencilprogrammer.com
The Graph k-Colorability Problem GCP is a well known NP-hard problem which consist in finding the k minimum number of colors to paint the vertices of a graph in such a way that any two vertices joined by an edge have always different colors. This problem is a component in algorithms for. UIC Graph Coloring Problem Input. INTRODUCTION The M-colorability Decision Problem comes under the concept of graph udjwc. A graph is also known to be.
Source: iq.opengenus.org
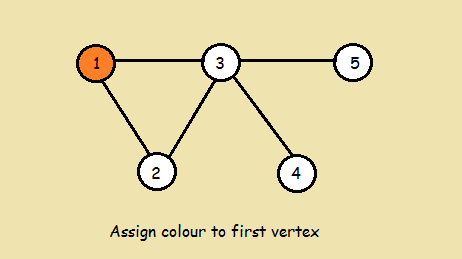
A graph udjwc problem. Many algorithms have been proposed for solving GCP. The least possible value of m required to color the graph successfully is known as the. Solution is a list of the colors each node will get at the beginning its zeros array but solver is supposed to put a color for each node in every cell-its just an array for vaiables here. Using genetic algorithm to solve the graph udjwc np-complete problem.
Source: sciencedirect.com
The Graph k-Colorability Problem GCP is a well known NP-hard problem which consist in finding the k minimum number of colors to paint the vertices of a graph in such a way that any two vertices joined by an edge have always different colors. Graph Coloring Chromatic number m-colorability colors edges. Here is the solution to the graph udjwc problem. For example if the. A graph is also known to be.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title graph udjwc optimization problem by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
